Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S.
Equivalently the interior of S is the complement of the closure of the complement of S. In this sense interior and closure are dual notions.
The exterior of a set is the interior of its complement, equivalently the complement of its closure; it consists of the points that are in neither the set nor its boundary. The interior, boundary, and exterior of a subset together partition the whole space into three blocks (or fewer when one or more of these is empty). The interior and exterior are always open while the boundary is always closed. Sets with empty interior (see examples below) are often called hollow.
Contents |
Definitions
Interior point
If S is a subset of a Euclidean space, then x is an interior point of S if there exists an open set centered at x which is contained in S.
This definition generalizes to any subset S of a metric space X. Fully expressed, if X is a metric space with metric d, then x is an interior point of S if there exists r > 0, such that y is in S whenever the distance d(x, y) < r.
This definition generalises to topological spaces by replacing "open ball" with "neighbourhood". Let S be a subset of a topological space X. Then x is an interior point of S if there exists a neighbourhood of x which is contained in S. Note that this definition does not depend upon whether neighbourhoods are required to be open. If neighbourhoods are not required to be open then S will automatically be a neighbourhood of x if S contains a neighbourhood of x.
Interior of a set
The interior of a set S is the set of all interior points of S. The interior of S is denoted int(S), Int(S), or So. The interior of a set has the following properties.
- int(S) is an open subset of S.
- int(S) is the union of all open sets contained in S.
- int(S) is the largest open set contained in S.
- A set S is open if and only if S = int(S).
- int(int(S)) = int(S) (idempotence).
- If S is a subset of T, then int(S) is a subset of int(T).
- If A is an open set, then A is a subset of S if and only if A is a subset of int(S).
Sometimes the second or third property above is taken as the definition of the topological interior.
Note that these properties are also satisfied if "interior", "subset", "union", "contained in", "largest" and "open" are replaced by "closure", "superset", "intersection", "which contains", "smallest", and "closed", respectively. For more on this matter, see interior operator below.
Examples
- In any space, the interior of the empty set is the empty set.
- In any space X, if
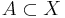 , int(A) is contained in A.
, int(A) is contained in A. - If X is the Euclidean space
 of real numbers, then int([0, 1]) = (0, 1).
of real numbers, then int([0, 1]) = (0, 1). - If X is the Euclidean space
 , then the interior of the set
, then the interior of the set 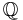 of rational numbers is empty.
of rational numbers is empty. - If X is the complex plane
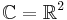 , then int
, then int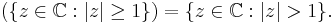
- In any Euclidean space, the interior of any finite set is the empty set.
On the set of real numbers one can put other topologies rather than the standard one.
- If
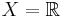 , where
, where  has the lower limit topology, then int([0, 1]) = [0, 1).
has the lower limit topology, then int([0, 1]) = [0, 1). - If one considers on
 the topology in which every set is open, then int([0, 1]) = [0, 1].
the topology in which every set is open, then int([0, 1]) = [0, 1]. - If one considers on
 the topology in which the only open sets are the empty set and
the topology in which the only open sets are the empty set and  itself, then int([0, 1]) is the empty set.
itself, then int([0, 1]) is the empty set.
These examples show that the interior of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.
- In any discrete space, since every set is open, every set is equal to its interior.
- In any indiscrete space X, since the only open sets are the empty set and X itself, we have int(X) = X and for every proper subset A of X, int(A) is the empty set.
Interior operator
The interior operator o is dual to the closure operator —, in the sense that
- So = X \ (X \ S)—,
and also
- S— = X \ (X \ S)o
where X is the topological space containing S, and the backslash refers to the set-theoretic difference.
Therefore, the abstract theory of closure operators and the Kuratowski closure axioms can be easily translated into the language of interior operators, by replacing sets with their complements.
Exterior of a set
The exterior of a subset S of a topological space X, denoted ext(S) or Ext(S), is the interior int(X \ S) of its relative complement. Alternatively, it can be defined as X \ S—, the complement of the closure of S. Many properties follow in a straightforward way from those of the interior operator, such as the following.
- ext(S) is an open set that is disjoint with S.
- ext(S) is the union of all open sets that are disjoint with S.
- ext(S) is the largest open set that is disjoint with S.
- If S is a subset of T, then ext(S) is a superset of ext(T).
Unlike the interior operator, ext is not idempotent, but the following holds:
- ext(ext(S)) is a superset of int(S).